The Wire, and Linear Algebra

Context

The Wire is a crime drama television show that documents the city of Baltimore in the early 2000s. It’s somewhat of an anthology series, where each season covers a different aspect of Baltimore’s institutions, and the first season (arguably the most popular) covers the illegal drug trade.

Pagers

There is a critical plot point in the first season about “the pager code” that the Barksdale crime organization uses. When the season first aired in 2002, pagers would’ve been commonplace and audiences would’ve been familiar with them, but now 23 years later, pagers have disappeared – and understanding how pagers work is critical to the plot.

I’ll vaguely explain how pagers work here.

When a user buys a pager, it comes with a phone number assigned to it. You give this phone number to other people, and they can call it just like a regular phone, except, instead of “ringing” your pager, the call goes straight to an operator, and you get prompted to enter a callback number. This number then appears on your pager’s display, as a way to say, “Hey, you got a call from this number. Call them back at your earliest convenience”.

In Season 1 Episode 5, as part of the police investigation, the detectives are allowed to clone one of the informant’s (D’Angelo Barksdale) pagers. They can then see the callback numbers that are shown on his pager.

Why the pager code is important

After receiving the numbers that show up on D’Angelo’s pagers, the police discover that the numbers are bogus, they do not map to real phone numbers. (Remember, the caller can enter the callback number, there is no automatic “Caller ID” type system). The police were able to observe D’Angelo receiving a page, then going to a payphone and placing a phone call - so they knew the number on the pager was coded somehow. At the time, pagers were only 7 digits, as you did not need an area code to dial someone, hence the additional difficulty.

Because of the Federal Wiretapping Act of 1968, the police could not simply record all calls made from a specific payphone in the hopes of catching D’Angelo. They needed to establish the identity of the callee - which cannot be done without linking the phone number to the person. Thus, the investigation would be stalled until the pager code was cracked – it would give them the real phone number of the callee - which they can use to establish the identity of the callee and thus legally record the call.

Explaining the code

The pager code is ultimately cracked by Detective Pryzbylewski. He discovers it to be a simple substitution cipher.

The key is that the cipher doesn’t require any memory of a complex key, it is all based on the layout of a standard number pad, as he describes it: “jumping the 5”.

Encrypted	Decrypted
1	9
2	8
3	1
4	6
5	0
6	4
7	3
8	2
9	1

The 5 is simply replaced with zero.

What’s neat about this system is that if you treat the phone keypad like a Cartesian coordinate system, where “5” is the origin, you can define the cipher in terms of a linear transformation.

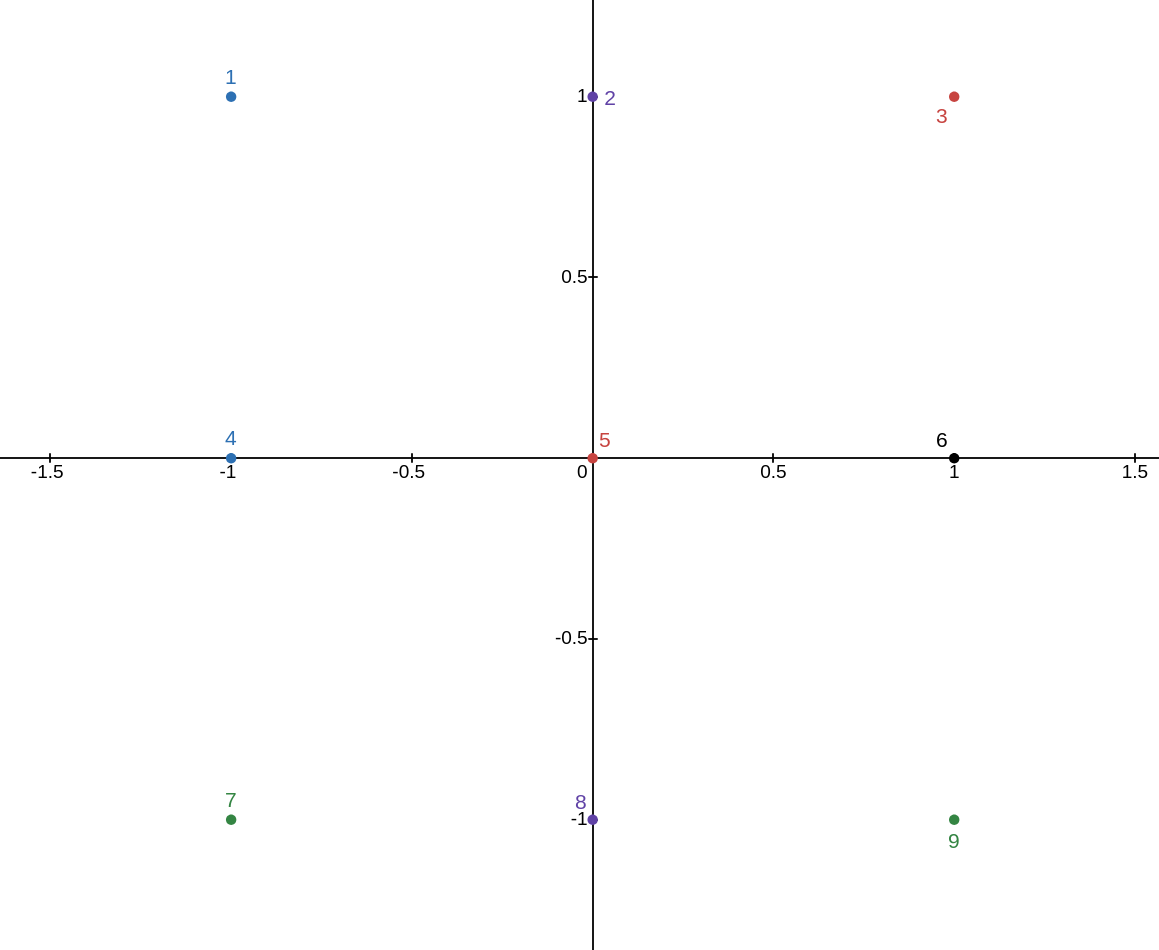
The cipher simply performs what is called a “reflection through the origin”, which is defined by the matrix:

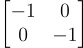
Code

If you want to play around with this cipher yourself, you can use the C program below:

#include <stdio.h>
#include <string.h>
#include <stdlib.h>

int main(int argc, char *argv[])
{

    if (argc != 2)
    {
        printf("Usage: %s <string>\n", argv[0]);
        return 1;
    }

    char *input_phone_num = argv[1];
    size_t input_str_length = strlen(input_phone_num);

    if (input_str_length < 7)
    {
        printf("Error! %zu is not enough digits to be a valid phone number. Must provide at least 7.\n", input_str_length);
        return 1;
    }
    else if (input_str_length > 10)
    {
        printf("Error! %zu is too many digits to be a phone number.\n", input_str_length);
        return 1;
    }
    else
    {
        const char substitution_map[10] = {'5', '9', '8', '1', '6', '0', '4', '3', '2', '1'};

        int idx = 0;

        for (idx = 0; idx < input_str_length; idx++)
        {
            const int digit = input_phone_num[idx] - '0'; // Convert char to int

            printf("%c", substitution_map[digit]);
        }
    }

    return 0;
}